קו הקואורדינטות. נקודות על קו הקואורדינטות. כיצד לבנות קו קואורדינטות

לומר שאתה יודע מתמטיקה היא בלתי אפשרית,אם אינך יודע איך לבנות גרפיקה, מייצגים אי-שוויון בקו-קואורדינטות, עבודה עם צירים של קואורדינטות. המרכיב החזותי במדע הוא בעל חשיבות מכרעת, שכן ללא דוגמאות ברורות בחישובים ובחישובים, אפשר לפעמים להתבלבל מאוד. במאמר זה, נבחן כיצד לעבוד עם צירים לתאם, וללמוד כיצד לבנות גרפים פונקציה פשוטה.

יישום

קו הקואורדינטות הוא הבסיס של המינים הפשוטים ביותרגרפים, אשר התלמיד פונה בדרכו החינוכית. הוא משמש כמעט בכל נושא מתמטי: בחישוב מהירות וזמן, הקרנת גודל של אובייקטים וחישוב השטח שלהם, ב trigonometry כאשר עובדים עם sines ו cosines.

הערך העיקרי של קו ישר כזה הוא הנראות. מאחר שהמתמטיקה היא מדע שבו נדרשת רמה גבוהה של חשיבה מופשטת, הגרפים מסייעים בייצוג של אובייקט בעולם האמיתי. איך הוא מתנהג? באיזו נקודה יהיה זה בעוד כמה שניות, דקות, שעות? מה אתה יכול להגיד על זה בהשוואה לאובייקטים אחרים? איזו מהירות יש לה בנקודה שנבחרה באקראי בזמן? כיצד לאפיין את תנועתו?

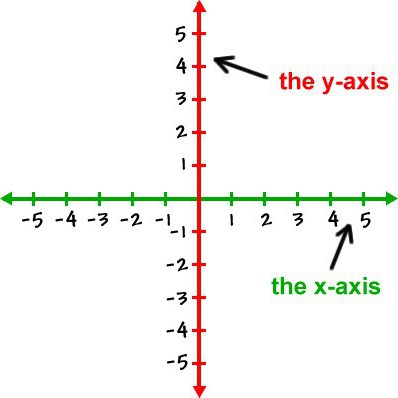
ועל המהירות זה לא בלי סיבה - זה היאלעתים קרובות להציג גרפים פונקציה. והם יכולים גם להציג שינוי טמפרטורה או לחץ בתוך האובייקט, ממדיו, כיוון יחסית לאופק. לכן, לעתים קרובות נדרש לבנות קו מתאם בפיסיקה.

תרשים חד-ממדי

יש רעיון של רב-ממדיות. במרחב חד מימדי, רק מספר אחד מספיק כדי לקבוע את המיקום של הנקודה. זה בדיוק המקרה עם השימוש בקואורדינטות. אם השטח הוא דו מימדי, אז שני מספרים נדרשים. תרשימים מסוג זה משמשים לעתים קרובות יותר, ועוד קצת במאמר אנו בהכרח לשקול אותם.

מה שאתה יכול לראות עם נקודות על הציר, אםהיא רק אחת? ניתן לראות את גודל האובייקט, את מיקומו בחלל ביחס לכמה "אפס", כלומר הנקודה שנבחרה כנקודת ההתייחסות.

שינוי הפרמטרים לאורך זמן לא ניתן לראות, שכן כל הסימנים יוצגו לרגע מסוים. אבל עם משהו שאתה צריך להתחיל! אז בואו נתחיל.

כיצד לבנות ציר קואורדינטות

ראשית, הוא נדרש לבצע אופקיקו - זה יהיה הציר שלנו. בצד ימין, "לחדד" את זה כדי שזה ייראה כמו חץ. לכן, אנו מציינים את הכיוון שבו המספרים יגדל. בכיוון של הפחתה, החץ הוא בדרך כלל לא מוגדר. באופן מסורתי, הציר מצביע ימינה, אז אנחנו פשוט בצע את הכלל הזה.

שים סימן אפס, אשר יהיהלהציג את מקור הקואורדינטות. זה המקום שממנו אתה סופר, אם זה גודל, משקל, מהירות או כל דבר אחר. בנוסף לאפס, אנחנו חייבים תמיד לייעד את מה שמכונה מחיר החלוקה, כלומר, להציג את התקן של היחידה, לפיה אנו נדחה כמויות מסוימות על הציר. זה חייב להיעשות על מנת להיות מסוגל למצוא את אורך קטע על קו קואורדינטות.

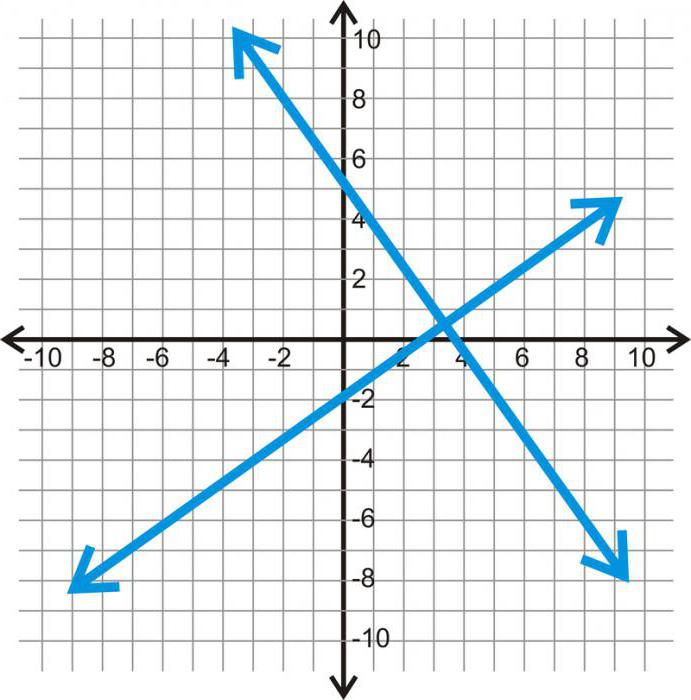
דרך מרחק שווה אחד מהשני שמנונקודות או "חריצים" על הקו, ומתחתם נכתוב 1,2,3 וכן הלאה, בהתאמה. ועכשיו הכל מוכן. אבל עם לוח הזמנים שהתקבל, אתה עדיין צריך ללמוד איך לעבוד.

סוגי נקודות על קו הקואורדינטות

במבט אחד על המוצע בספרי הלימודהדמויות מתבהרות: הנקודות על הציר יכולות להיות צבועות או לא צבועות. אתה חושב שזו תאונה? בכלל לא! נקודה "מוצקה" משמשת לאי שוויון לא קפדני - נפח הנקרא "גדול או שווה". אם יש צורך להגביל לחלוטין את המרווח (לדוגמה, "x" יכול לקחת ערכים מאפס לאחד, אך אינו כולל אותו), אנו משתמשים בנקודה "חלולה", כלומר, מעגל קטן על הציר. יש לציין שהתלמידים לא אוהבים חוסר שוויון קפדני, כי קשה יותר לעבוד איתם.

תלוי באיזו נקודה אתה משתמשעל הגרף, יקראו ואת המרווחים שנבנו. אם אי השוויון הוא לא קפדני משני הצדדים, אז אנחנו מקבלים קטע. אם, מצד אחד, הוא "פתוח", אז זה ייקרא חצי מרווח. לבסוף, אם חלק של קו ישר הוא כבול משני הצדדים על ידי נקודות חלולות, זה ייקרא מרווח.

מטוס

בעת בניית שתי שורות בקואורדינטההמטוס, אנחנו כבר יכולים לשקול את גרפים של פונקציות. לדוגמה, הקו האופקי יהיה ציר הזמן, וקו אנכי יהיה המרחק. ועכשיו אנחנו יכולים לקבוע איזה מרחק האובייקט יהיה להתגבר על דקה או שעה של הדרך. לפיכך, עבודה עם מטוס מאפשרת לפקח על מצב האובייקט. זה הרבה יותר מעניין מאשר לחקור מצב סטטי.

הגרף הפשוט ביותר על מטוס כזה הוא קו ישר, הוא משקף את הפונקציה Y (X) = aX + b. האם קו כיפוף? משמעות הדבר היא שהאובייקט משנה את מאפייניו בתהליך המחקר.

תאר לעצמך שאתה עומד על גג של בניין ולשמורביד מושטת אבן. כאשר אתה משחרר את זה, זה יהיה לטוס למטה, החל במהירות אפס. אבל בתוך שנייה הוא יגבר 36 ק"מ לשעה. האבן תמשיך להאיץ עוד יותר, וכדי לצייר את התנועה שלה על הגרף, תצטרך למדוד את מהירותה בכמה נקודות זמן, לשים את הנקודות על הציר במקומות המתאימים.

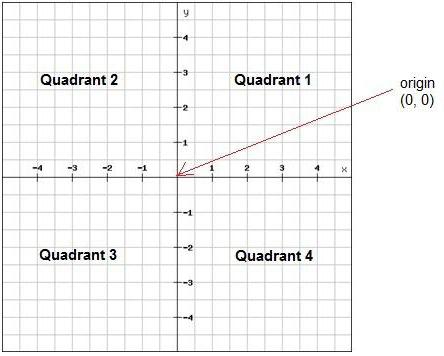
הסימנים בשורת הקואורדינטות האופקיות מופעליםשם ברירת המחדל הוא X1, X2, X3, ועל אנכי - Y1, Y2, Y3, בהתאמה. הקרנה על המטוס ומציאת צמתים, אנו מוצאים שברי דפוס שהתקבל. על ידי שילובם עם שורה אחת, אנו מקבלים גרף של הפונקציה. במקרה של אבן נופלת, הפונקציה הריבועית תהיה בצורת: Y (X) = aX * X + bX + c.

זום

כמובן, אין צורך להציג לידחלוקה לפי ערכים שלמים שלמים. אם אתה שוקל את התנועה של שבלול, אשר זוחל במהירות של 0.03 מטרים לדקה, להגדיר את הערכים בקו ישר קואורדינטות כמו שברים. במקרה זה, לקבוע את מחיר החלוקה כ 0.01 מטר.

זה נוח במיוחד לבצע רישומים כאלה במחברתבכלוב - כאן אתה יכול מיד לראות אם יש מספיק מקום על הסדין עבור לוח הזמנים שלך, לא תעזוב את השדות. כוחו לחשב הוא פשוט, כי רוחב התא במחברת כזו הוא 0.5 ס"מ. זה היה הכרחי - צמצמו את הדמות. מהשינוי בסולם הסקירה, הוא לא יפסיד ולא ישנה את תכונותיו.

נקודות ציון של נקודה ופלח

כאשר השיעור נותן בעיה מתמטית, בזה יכול להכיל פרמטרים של דמויות גיאומטריות שונות הן בצורה של אורכים של הצדדים, היקף, שטח, בצורה של קואורדינטות. במקרה זה, ייתכן שיהיה עליך לבנות דמות, ולקבל כמה נתונים הקשורים אליו. נשאלת השאלה: איך למצוא את המידע הדרוש על קו הקואורדינטות? ואיך לבנות דמות?

לדוגמה, אנחנו מדברים על נקודה. האות ההונית תופיע במצב הבעיה, ובסוגריים יהיו מספר ספרות, בדרך כלל שתיים (כלומר, נספור בחלל דו-מימדי). אם יש שלושה מספרים בסוגריים שנכתבו באמצעות נקודה פסיק או פסיק, זהו מרחב תלת-ממדי. כל אחד מהערכים הוא הקואורדינטות על הציר המתאים: תחילה לאורך האופקי (X), ולאחר מכן על האנכי (Y).

זוכר איך לבנות חתיכת? עברת את זה על הגיאומטריה. אם יש שתי נקודות, אז אתה יכול לצייר קו ישר ביניהם. הקואורדינטות שלהם מסומנות בסוגריים, אם קטע מופיע בבעיה. לדוגמה: A (15, 13) - B (1, 4). כדי לבנות קו כזה, אתה צריך למצוא ולסמן נקודות על המטוס קואורדינטה, ולאחר מכן לחבר אותם. זה הכל!

וכל פוליגונים, כפי שאתה יודע, ניתן לצייר בעזרת קטעים קו. הבעיה נפתרת.

חישובים

נניח שיש אובייקט, מיקוםהמאופיינת בשני מספרים לאורך ציר ה- X: היא מתחילה בנקודה עם הקואורדינטת (-3) ומסתיימת ב- (+2). אם אנחנו רוצים לדעת את אורך האובייקט הזה, אז אנחנו חייבים להפחית את מספר קטן יותר. שים לב כי מספר שלילי סופג את סימן החיסור, כי "מינוס נותן יתרון". אז, אנו מוסיפים (2 + 3) ולקבל 5. זוהי התוצאה הנדרשת.

דוגמה נוספת: אנו מקבלים את נקודת הסיום ואת האורך של האובייקט, אבל לא הראשון (וזה נדרש למצוא אותו). תנו את המיקום של נקודת ידוע להיות (6), ואת הגודל של האובייקט למד - (4). הפחתת אורך מן הקואורדינטות סופיות, אנחנו מקבלים את התשובה. סה"כ: (6 - 4) = 2.

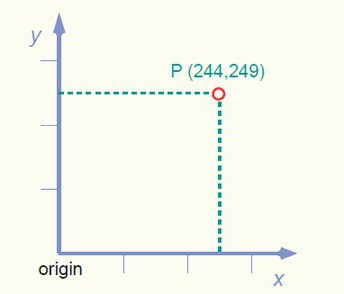
מספרים שליליים

זה נדרש לעתים קרובות לעבוד עםערכים שליליים. במקרה זה, נלך לאורך ציר הקואורדינטות משמאל. לדוגמה, אובייקט 3 ס"מ גבוה צף במים. בשלישית, הוא שקוע נוזלי, שני שלישים הוא באוויר. לאחר מכן, בבחירת פני המים כציר, אנו משתמשים בשני מספרים בסיסיים כדי לחשב את פני השטח של האובייקט: בראש האובייקט יש קואורדינטות (+2), ואת החלק התחתון (-1) סנטימטר.

זה לא קשה לראות את זה במקרה של yאנחנו נוצרים ארבעה רבעים של קו הקואורדינטות. לכל אחד מהם יש מספר משלו. בחלק הראשון (מימין למעלה) יהיו נקודות עם שתי קואורדינטות חיוביות, בשנייה - בצד שמאל למעלה - הערכים לאורך ציר "x" יהיו שליליים, ועל פי "איגריק" חיובי. השלישי והרביעי נספרים עוד נגד כיוון השעון.

נכס חשוב

אתה יודע כי קו ישר ניתן לדמייןאינסופי של נקודות. אנחנו יכולים להסתכל על כל מספר של ערכים ככל שאנו רוצים לכל צד של הציר, אבל אנחנו לא נפגשים חוזרים. זה נראה נאיבי ומובן, אבל אמירה זו נובעת מעובדה חשובה: לכל מספר יש נקודת אחת ונקודה אחת בלבד בקו התיאום.

מסקנה

זכור כי כל הצירים, הצורות, ואם אפשר,גרפיקה חייב להיות בנוי על פי השליט. יחידות של מדידות הומצאו על ידי אדם לא במקרה - על ידי ביצוע טעות ב שרטוט, אתה מסתכן לראות את התמונה לא היה צריך להתברר.

היזהר וזהיר בבנייןגרפים וחישובים. כמו כל מדע שנלמד בבית הספר, מתמטיקה אוהבת דיוק. צרף קצת מאמץ, וציונים טובים לא ייקח הרבה זמן.