אורך אקורד: מושגים בסיסיים
ישנם מקרים בחיים כאשר הידע שנרכשבמהלך החינוך בבית הספר, הם מאוד שימושי. אמנם במהלך המחקר מידע זה נראה משעמם ומיותר. לדוגמה, כיצד ניתן להשתמש במידע אודות האורך של אורך האקורד? יש להניח כי עבור התמחויות שאינן קשורות למדעים המדויקים, ידע זה מועט. עם זאת, אתה יכול לתת דוגמאות רבות (מתוך עיצוב תחפושת השנה החדשה למכשיר מטוס מורכב), כאשר המיומנויות בפתרון בעיות בגיאומטריה אינם מיותרים.
הרעיון של "אקורד"
מילה זו פירושה "מחרוזת" בתרגום משפת המולדת של הומרוס. זה היה הציג על ידי מתמטיקאים של התקופה העתיקה.

חלק מהמטוס מוקף בקו ישר,חוצה מעגל, והקשת שלו נקראת פלח. ניתן לציין כי אורך אקורד עולה עם הגישה למרכז. חלק ממעגל בין שתי נקודות של צומת של קו נתון נקרא arc. מדד המדידות שלה הוא הזווית המרכזית. הקודקוד של הדמות הגיאומטרית הזאת נמצא באמצע המעגל, והצדדים נמצאים על נקודות הצומת של האקורד עם המעגל.
מאפיינים ונוסחאות
אורך האקורד של מעגל ניתן לחשב לפי הביטויים המותנים הבאים:
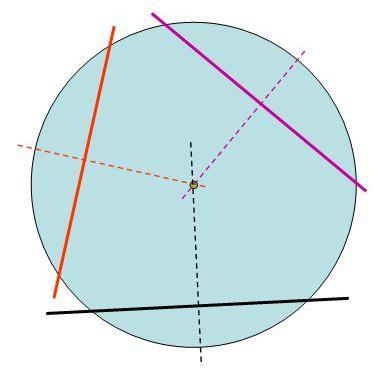
L = D = Sinβ או L = D = חטא (1 / 2α), כאשר β היא הזווית בקודקוד המשולש.
D הוא קוטר המעגל;
α היא הזווית המרכזית.
אתה יכול לבחור כמה מאפיינים של קטע זה, כמו גם דמויות אחרות הקשורות אליו. נקודות אלה מפורטות ברשימה הבאה:
- כל אקורדים הנמצאים באותו מרחק מהמרכז יש אורכים שווים, ואת ההצהרה הפוך גם נכון.
- כל הזוויות שנרשמו במעגל ונתמכות על ידי מקטע משותף המשלב שתי נקודות (קודקודן בצד אחד של אלמנט זה) זהות זה מזה.
- האקורד הגדול ביותר הוא הקוטר.
- סכום של כל זווית, אם הם נתמכים על ידי מקטע מסוים, אבל הקודקודים שלהם שוכבים בצדדים שונים ביחס אליו, הוא 180o.
- האקורד הגדול - בהשוואה לאלמנט דומה, אך קטן יותר - נמצא קרוב יותר לאמצע הדמות הגיאומטרית.
- כל הזוויות שנכתבות ונתמכות בקוטר 90 °.
חישובים אחרים
כדי למצוא את אורך קשת של המעגל, אשר סגורה בין הקצוות של אקורד, אתה יכול להשתמש בנוסחה Huygens. לשם כך יש לבצע את הפעולות הבאות:

- ציין את הערך הנדרש של p, ואת אקורד כי גבולות זה חלק של המעגל יהיה שם AB.
- אנו מוצאים את האמצע של קטע AB ו לשים אותו אליובניצב. ניתן לציין שקוטר המעגל שצויר דרך מרכז האקורד יוצר זווית ישרה עמו. גם ההיפך הוא הנכון. במקרה זה, הנקודה שבה הקוטר, עובר באמצע האקורד, נוגע במעגל, מסומן על ידי מ '.
- ואז את המגזרים AM ו- BM ניתן לקרוא בהתאמה, כמו l ו- L.
- אורך קשת יכול להיות מחושב מהפעולות הבאותנוסחה: p≈2l + 1/3 (2l-L). ניתן לציין כי השגיאה היחסית של ביטוי זה עולה עם זווית גוברת. לכן, ב 60 ° זה 0.5%, ועל arc שווה ל 45 מעלות ערך זה יורד ל 0.02%.
אורך אקורד ניתן להשתמש במגווןספירות. לדוגמה, בחישוב ועיצוב של חיבורי אוגן, אשר נמצאים בשימוש נרחב בהנדסה. אתה יכול גם לראות את החישוב של ערך זה בבליסטיקה כדי לקבוע את המרחק של הטיסה כדור וכדומה.