פעולות לוגיות הפשוטות ביותר במדעי המחשב

כל מי שמתחיל ללמוד מדעי המחשב נלמדמערכת בינארית של חצץ. הוא משמש לחישוב פעולות לוגיות. בואו ניקח בחשבון את כל הפעולות הבסיסיות ביותר בתחום הלוגי במדעי המחשב. אחרי הכל, אם אתה חושב על זה, הם משמשים בעת יצירת ההיגיון של מחשבים והתקנים.

הכחשה

לפני שנתחיל לשקול בפירוט דוגמאות ספציפיות, אנו מונה את הפעולות הלוגיות העיקריות במדעי המחשב:

• שלילה;
• An קבוצה
• כפל;
• בצע;
• שוויון.

כמו כן, לפני תחילת המחקר הלוגי פעולות, כדאי לומר כי במדעי המחשב שקר מיועד "0", והאמת היא "1".

עבור כל פעולה, כמו במתמטיקה רגילה, נעשה שימוש בסימנים הבאים של פעולות לוגיות במידע: ¬, v, &, ->.

כל פעולה יכולה להיות מתוארת על ידי 1/1 ספרות, או פשוט על ידי ביטויים לוגיים. בואו נתחיל עם לוגיקה מתמטית עם פעולה פשוטה שמשתמשת רק במשתנה אחד.

שלילה לוגית היא פעולת היפוך. השורה התחתונה היא שאם הביטוי המקורי נכון, התוצאה של ההיפוך היא שקרית. לעומת זאת, אם הביטוי המקורי הוא שקר, התוצאה של היפוך יהיה נכון.

בעת כתיבת ביטוי זה, נעשה שימוש בסימון הבא: "¬A".

הנה טבלת אמת - דיאגרמה המציגה את כל התוצאות האפשריות של ניתוח עבור כל נתוני קלט.

טבלת האמת עבור היפוך

א	x	o
¬A	o	x

כלומר, אם הביטוי המקורי שלנו הוא נכון (1), אז שלילתו תהיה שקרית (0). ואם הביטוי המקורי הוא שקר (0), אז שלילתו נכונה (1).

תוספת

שאר הפעולות דורשות שני משתנים. אנו מציינים ביטוי אחד -

השני - V. פעולות לוגיות ב אינפורמטיקה, אשר מציינים את התוספת (או disjunction), מסומנים על ידי סימן המילה "או" או "V". בואו נכתוב את אפשרויות הנתונים האפשריות ואת תוצאות החישובים.

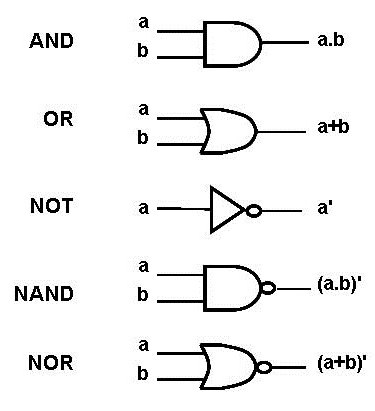
1. E = 1, H = 1, ולאחר מכן E = H = 1. אם שתי הביטויים נכונים, אז הפרדתם נכונה גם כן.
2. E = 0, H = 1, אז E = H = 1. E = 1, H = 0, אז E = H = 1. אם לפחות אחת מההבעות נכונה, התוצאה של התוספת תהיה נכונה.
3. E = 0, H = 0, התוצאה היא E = H = 0. אם שתי הביטויים שקר, אז הסכום שלהם הוא גם שקר.

עבור קיצור, ליצור טבלת האמת.

ניתוק

ה	x	x	o	o
ח	x	o	x	o
E v H	x	x	x	o

כפל

לאחר שעסק המבצע של תוספת, ללכתכפל (יחד). אנו משתמשים באותה סימוכין כמפורט לעיל. בעת הכתיבה, הכפל הלוגי מסומן על ידי הסמל "&" או האות "AND".

1. E = 1, H = 1, ואז E & H = 1. אם שתי הביטויים נכונים, אז שלהם יחד הוא נכון.
2. אם לפחות אחד הביטויים הוא שקר, אז התוצאה של כפל לוגי יהיה גם שקר.

• E = 1, H = 0, ולכן E & H = 0.
• E = 0, H = 1, ואז E & H = 0.
• E = 0, H = 0, תוצאה של E & H = 0.

יחד

ה	x	x	0	0
ח	x	0	x	0
E & H	x	0	0	0

תוצאה

הניתוח הגיוני לוגי (משתמע) הוא אחד ההיגיון הפשוט ביותר במתמטיקה. הוא מבוסס על אקסיומה אחת - האמת אינה יכולה להיות מלווה בשקר.

1. E = 1, H =, ולכן E -> H = 1. אם בני הזוג מאוהבים, אז הם יכולים לנשק - את האמת.
2. E = 0, H = 1, ואז E -> H = 1. אם בני הזוג אינו מאוהב, אז הם יכולים לנשק - זה יכול גם להיות נכון.
3. E = 0, H = 0, מכאן E -> H = 1. אם בני הזוג לא מאוהבים, אז הם לא מנשקים - זה גם נכון.
4. E = 1, H = 0, התוצאה היא E -> H = 0. אם בני הזוג מאוהבים, אז הם לא מנשקים - זה שקר.

כדי להקל על יישום של פעולות מתמטיות, אנחנו גם נותנים טבלת האמת.

משמעות

ה	x	x	o	o
ח	x	o	x	0
E -> H	x	o	x	x

שוויון

המבצע האחרון נחשב יהיהזהות לוגית או שוויון. בטקסט, זה יכול להיות מיועד "... אם ורק אם ...". בהצעת ניסוח זה, נכתוב דוגמאות לכל הווריאציות הראשוניות.

1. A = 1, B = 1, ואז A≡B = 1. אדם שותה טבליות רק אם הוא חולה. (נכון)
2. A = 0, B = 0, בסופו של דבר A≡B = 1. אדם אינו שותה טבליות אם ורק אם הוא לא חולה. (נכון)
3. A = 1, B = 0, כך A≡B = 0. אדם שותה טבליות רק אם הוא לא מקבל חולה. (שקר)
4. A = 0, B = 1, ואז A≡B = 0. אדם לא לוקח גלולות אם ורק אם הוא חולה. (שקר)

שוויון

א	x	o	x	o
ב	x	o	0	x
A≡B	x	x	o	o

מאפיינים

אז, לאחר שוקלים את הפעולות הפשוטות ביותר לוגי באינפורמטיקה, אנחנו יכולים להתחיל ללמוד כמה נכסים שלהם. כמו במתמטיקה, פעולות לוגיות יש סדר עיבוד משלהם. בביטויים לוגיים גדולים, הפעולות בסוגריים מבוצעות תחילה. אחריהם, קודם כל, אנחנו מחשבים את כל הערכים של שלילה בדוגמה. השלב הבא הוא לחשב את יחד, ואז disjunction. רק אחרי זה אנחנו מבצעים את הניתוח של החקירה, ולבסוף, את השקילות. חשבו על דוגמה קטנה לבהירות.

A B B & B B -> B ≡ A

סדר הפעולה הוא כדלקמן.

1. ¬В
2. B & B (¬ B)
3. V (B & B)
4. (A) (B & B)))) → B
5. ((A (B & B ¬ B))) -> B) ≡ A

כדי לפתור את הדוגמה הזאת, אנויהיה עליך לבנות טבלת האמת המורחבת. כאשר אתה יוצר את זה, זכור כי עדיף למקם את העמודות באותו סדר שבו הפעולות יבוצעו.

פתרון לדוגמה

א	ב	¬В	B & B (¬ B)	V (B & B)	(A) (B & B)))) → B	((A (B & B ¬ B))) -> B) ≡ A
x	o	x	o	x	x	x
x	x	o	o	x	x	x
o	o	x	o	o	x	o
o	x	o	o	o	x	o

כפי שאנו רואים, העמודה האחרונה תביא לפתרון של הדוגמה. טבלת האמת סייעה לפתור את הבעיה עם נתונים ראשוניים אפשריים.

מסקנה

במאמר זה, כמה מושגים כבר נחשבלוגיקה מתמטית, כגון אינפורמטיקה, תכונות של פעולות לוגיות, וכן - מה הם פעולות לוגיות כשלעצמם. כמה דוגמאות פשוטות ניתנו לפתרון בעיות לוגיות מתמטיות ולטבלאות האמת הנחוצות כדי לפשט את התהליך.